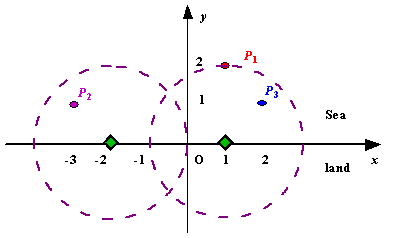
Assume the coasting is an infinite straight line. Land is in one side of coasting, sea in the other. Each small island is a point locating in the sea side. And any radar installation, locating on the coasting, can only cover d distance, so an island in the sea can be covered by a radius installation, if the distance between them is at most d.
We use Cartesian coordinate system, defining the coasting is the x-axis. The sea side is above x-axis, and the land side below. Given the position of each island in the sea, and given the distance of the coverage of the radar installation, your task is to write a program to find the minimal number of radar installations to cover all the islands. Note that the position of an island is represented by its x-y coordinates.
Input
The input consists of several test cases. The first line of each case contains two integers n (1<=n<=1000) and d, where n is the number of islands in the sea and d is the distance of coverage of the radar installation. This is followed by n lines each containing two integers representing the coordinate of the position of each island. Then a blank line follows to separate the cases.
The input is terminated by a line containing pair of zeros
Output
For each test case output one line consisting of the test case number followed by the minimal number of radar installations needed. "-1" installation means no solution for that case.
Sample Input
3 2
1 2
-3 1
2 1
1 2
0 2
0 0
Sample Output
Case 1: 2
Case 2: 1各ポイントをx軸に「投影」します。ここで、投影とは、そのポイントまでスキャンするレーダーをマークするx軸上のオプションの位置を指します。 実装に関しては、この範囲のレーダーは変化点をスキャンできます。 したがって、質問は、質問のコンテキストに合うように、間隔に含まれるポイントの数に変換されます。
次に、左から右に、間隔の左側が前の間隔に埋め込まれている場合、これら2つの間隔に必要なレーダーは1つだけです。 複数のアナロジー。 したがって、左から右にトラバースします(この間隔の左右の配置は、間隔の右端点の左右の配置です)。次の間隔の左側がこの間隔の右側よりも小さい場合、次の間隔は無視して計算できません。
#include <iostream>
#include <algorithm>
#include <cmath>
#include <vector>
using namespace std;
struct interval{
double start;
double end;
bool being_occupied;
};
vector<interval> inter;
bool cmp(interval a,interval b){
return a.end<b.end;
}
int main(){
// freopen("TrueExample.txt","r",stdin);
// freopen("Out.txt","w",stdout);
for(int example=1;;example++){
inter.clear();
int n,d;
cin >> n >> d;
if(n==0&&d==0) return 0;
bool can_t=false;
if(d<0) can_t=false;
for(int i=0;i<n;i++){
int px,py;
cin >> px >> py;
if(py>d) can_t=true;
interval I;
I.being_occupied=false;
I.start=(double)px-sqrt(d*d-py*py);
I.end=(double)px+sqrt(d*d-py*py);
inter.push_back(I);
}
if(can_t){
cout << "Case " << example << ": -1" << endl;
continue;
}
sort(inter.begin(),inter.end(),cmp);
int points=0;
for(int i=0;i<inter.size();i++){
if(inter[i].being_occupied) continue;
inter[i].being_occupied=true;
for(int j=i+1;j<inter.size();j++){
if(inter[j].start<=inter[i].end){
inter[j].being_occupied=true;
}
if(inter[j].start>inter[i].end) break;
}
points++;
}
cout << "Case " << example << ": " << points << endl;
}
}
これがクールな例です:
2 5
-3 4
-6 3
4 5
-5 3
-3 5
2 3
3 3
20 8
-20 7
-18 6
-5 8
-21 8
-15 7
-17 5
-1 5
-2 3
-9 6
1 2
2 3
3 4
4 5
5 6
6 7
7 8
8 7
9 6
10 5
0 0
2 3
0 2
2 3
2 3
0 2
1 3
3 3
1 2
-3 2
2 4
8 5
2 4
-4 4
-3 3
-3 1
-3 0
-1 0
0 5
6 0
3 0
1 2
-3 1
2 1
3 2
1 2
-3 1
2 1
1 2
0 2
2 3
0 2
2 3
4 -5
4 3
4 3
2 3
6 -9
3 -3
1 2
-3 2
2 1
6 2
1 2
1 2
1 2
-3 1
2 1
0 0
1 2
0 2
2 3
0 2
1 3
3 10
1 10
2 3
4 5
3 5
1 10
2 3
4 5
4 7
1 10
2 3
4 5
0 0
3 9
1 10
2 3
4 5
0 0これがクールな出力です:
case 1: 1
case 2: 2
case 3: 4
case 4: 1
case 5: 1
case 6: -1
case 7: 3
case 8: -1
case 9: 2
case 10: 1
case 11: 1
case 12: -1
case 13: -1
case 14: 2
case 15: 1
case 16: 1
case 17: 1
case 18: -1
case 19: -1
case 20: -1
コメント